My interests are my castle!

Rafi Blumenfeld: Research plans / main interests

The following list is in constant evolution. The highlighted words will send you to somewhat more detailed decriptions of the approaches that I take / intend to take / would like to take in addressing these problems. This page is updated rather slowly, but it gives a flavour of what I have been doing. Since the list covers a rather broad range of interests progress is limited to current pet problems. I therefore welcome discussions that may either result in collabotaions or get others involved in some of these ideas.

Current interests

• Granular media and cellular systems: stress transmission, statistical mechanics and flow
  
  On our theory of self-organisation of granular media paper1
  
  Move them to jostle and shear them to slide
  Granules constantly rub and collide
  Cells split and diffuse
  Theorists to bemuse
  But now we can see how they self-organise
  (RB April 2019)
  
  Stress transmission:
  This work is relevant to many industries: powders, grain transport, mechanical and flow properties of sand, colloidal suspensions, mechanics of solid foams, and even stress transmission in biological cells. It has been recognised that to understand the rich behaviour of granular matter it is essential to have a fundamental theory of isostatic stress states. These are stress states in idealised structures, in which the forces between elements of the system (grains, struts, colloids) are statically determinate, making these structures marginally rigid. They are significant because it has been argued that real granular materials should be regarded as two-phase composites of isostatic and over-connected regions [2]. This has been shown using a very low-tech experiment [10], where we verified that isostatic states are easy to access and that they affect non-isostatic materials. Isostatic media cannot be described by elasticity theory and they support what is known as force chains or arches. The relevant stress equations describing such behaviour are called isostaticity theory. We have shown also that the marginally rigid state acts as a critical point [10], which has profound effects for the understanding of granular matter in general. We formulated a first-principles mesoscopic isostaticity theory [1], identifying constitutive stress-structure properties in two-dimensional isostatic systems of rough and smooth rigid particles. The theory decouples the stress field from any deformation-related information. The equations are coarse-grainable straightforwardly only for a special subset of disordered microstructures, which we called un-frustrated, a term taken from antiferromagnetic spin system. However, eventually, a special method was constructed to coarse-grain the equations for general isostatic system [11].
  More recently, we found solutions for the Cartesian-based isostaticity equations in general media [6]. These solutions showed that stress is not supported only by chins but also `spills' to teh rest of teh system, when the structure is disordered [2,6].
  With the insight gained from our theoretical and experimental results we have proposed a first-principles set of equations for the way that granular matter yields and flows under an increasing load. All this work is carried out both theoretically and numerically. [1], [2], [3], [4], [5], [6], [7], , [8], [9], [10], [11], [12] [13].
  As is sometimes the case when fundamental science is involved paradigms are shifted. The project has started to branch out in several exciting directions and the flood of new results far exceeds the rate of paper production. One interesting development is a direct mapping between the structure of granular assemblies at the marginal rigidity state and skeletal cellular systems [12]. This makes it possible to apply the entropic formalism directly to cellular systems [13]. The work on structurally irregular cellular systems is of relevance in many fields of research, as well as for a wide range of technological applications. In particular, some of this work makes it possible to model metal, plastic and biomimetic foams, materials that are central in many technological applications. It also makes it possible to derive constitutive properties in porous materials, another class of technologically relevant materials.
  
  
  Selected milestones:
  
• 3D missing equations - Derivation of the missing constitutive equations for the stress field for three dimensional quadrivalent open-cell systems, a mapping between this and three dimensional granular assemblies at the marginal rigidity state and therefore the equation applies to the latter msterials as well. This paper is in preparation. (Dec02)
• Coarse-graining - Coarse-graining of the Ball-Blumenfeld constitutive equation in two dimensional systems, which has been derived on the scale of a few grains. The equation now applies to macroscopic lengthscales with smoothed upscaled coefficients which, unlike the coefficients on the granular/cellular scale, have a finite volume average. (Jan 03)
• 2D code - Development of a small code that analyses two-dimensional solid foams and outputs the relevant fabric tensors and entropic-related properties, such as the free porosity, mean porosity and porosity fluctuations. If you want me to analyse your foam structure with this code you need to send me the data in this format. This code will also tell you how many elliptic defects the foam has, if any. No paper yet but some exciting work on liquid crystalline foams with Seb Courty is under way - watch this space! (Jun 03)
• Solution and Green function of the stress eqs. in 2D - Derivation of the equations for the stress components on lengthscales just larger than a few grains. All the stress components are found to follow an identical hyperbolic equation but with different source terms. The Green function for an infinite medium has been derived and the general solution of the equations has been found. The solutions give rise naturally to force chains that follow the trajectories of the characteristic lines of the solution. The trajectories and magnitudes of the force chains have then been predicted in terms of the local geomtry. This has been published in (Phys. Rev. Lett., 93, 108301 (2004). (Oct 03)
• Emulsions - Experimental studies (not mine) of packings of droplets in emulsions are relevant in that they behave in some circumstances as granular systems. An interesting recent technique, developed by Jasna Brujic, exploits confocal microscopy imaging to yield provide the distributions of both the forces between droplets and the coordination numbers. These make it possible to compute the stress field in a compressed emulsion. The techniques are described in Jasna Brujic's thesis. (Jul 04)
• Jamming calculation in 2D - The phenomenon of jamming of granular packings under shear has been long associated with force chains. Using isostaticity theory, I have recently derived the magnitudes and directions of the force chains developing under such conditions in two-dimensional sheared assemblies of grains. A preprint on this is in its final draft form. (Oct 04)
• Application of isostaticity theory to non-rigid grains - Much controversy still surrounds the applicability of isostaticity theory granular packings to real systems. One of the objections is that, while the ideal theory discussed infinitely rigid grains, real grains always have a finite rigidity, however high. My view is that if the rigidity of the grains is sufficiently high then isostaticity theory is relevant, albeit with small elastic corrections. This idea is explored in a recent paper, Stress transmission and isostatic states of non-rigid particulate systems, that demonstrates how isostaticity theory applies to systems of compliant grains as long as they satisfy the topolgical constraint of static determinacy. (Dec 04)
• Application of entropic characterisation to structure-property relations in porous media - An exciting three-year research proposal that I have put up on this subject together with Profs Peter King and Martin Blunt of Imperial College, "Skeletonisation, entropic characterisation and conductivity-permeability relationship in porous media", has been funded recently. (the original page on the EPSRC site is here but I am not sure how long it would stay there).
  (Jan 05)
• Entropic formalism of three-dimensional cellular structures - The entropic formalism has been extended from two- to three-dimesional cellular and granular structures. The use of statistical mechanical methods, based on Edwards' compactivity concept, for such systems has remained underdeveloped because: (a) it has been unclear why an equlibrium-based description should apply to non-equilibrium evolving structures, such as soap froths and foams; (b) it has been difficult to identify a phase space that makes it possible to either disentangle the geometrical correlations or at least enable to treat them systematically; (c) it has been unclear what should play the role of a Hamiltonian, which is at the foundation of the conventional statistical mechanical formalism; (d) the extension of the concept of temperature is far from obvious in these a-thermal systems. In a recent paper, entitled "Geometric partition functions of cellular systems: Explicit calculation of the entropy in two and three dimensions", we resolve these difficulties. A key ingredient that makes this possible is a new way to partition the volume of cellular structures. This method appears to be useful to countless other applications. (e) it is October 2011 and the physics of granular matter is still poorly understood. The use of statistical mechanics is the one most significant issue that can jump-start derivation of desperately needed equations of state and constitutive relations of such matter. We have just submitted a paper showing that many of the results in the field of statistical mechanics of granular matter have been based on the wrong presumption that the volume ensemble is sufficient to describe the entropy of granular matter. We demonstrate that both the volume and the stress ensembles are not only required but also inter-dependent. We then present several correct calculations. Finally and significantly, we show that statistical mechanics of granular matter support an equipartition principle, in contrast to a number of recent publications, including in Phys.Rev.Lett., which claim the opposite.
• Applications to strains in auxetic materials - There are many similarities between dilatancy in granular systems and strains in open cell and auxetic structures. Both systems involve local rotations of basic building blocks which gives rise to non-affine deformations. A local equation that relates the strain in auxetic materials to the stress has been derived recently for two-dimensional structures. The equation is valid to all auxetic structures, disordered as well as ordered. However, since the stress solutions differ significantly between conventional auxetic materials (which I term elasto-auxetic) and iso-auxetic structures - structures that are both isostatic and auxetic - then the dynamics should be significantly different between the two classes of materials. A paper on this issue, entitled "Auxetic strains - insight from iso-auxetic materials", has appeared recently in Molecular Simulation. The extension of the formalism to three dimensions is doable in my opinion and will be reported eventually. (Jun 05)
  This extension has been done and reported in 2012 (see publication list).
  This is also related somewhat to the issue of `frustration' in granular systems, which I will write about eventually. Until then, here is a sketch of an unfrustrated part of a particulate assembly.
  
  
On modeling Disordered Auxetics
On pulling they swell, on pushing they dense
Auxetic materials defy common sense
They expand and dilate
Causing heated debate
But iso-auxeticity dispels the suspense
(RB June 2015)


• Applications to force mediation in biological cells - Mediation of forces is probably the one most general mechanism of signalling in all biological cells and this is done via the cytoskeleton. Conventional continuous models of stresses have been found to fall short of explaining observations of 'action at a distance' upon applying a force to particular receptors on the membrane. I have shown that there are several advantages for cells to transmit such stimuli in a focused manner and argued that the tendency in the biological community to reject continuous models on the basis of these observations is flawed. In particular, I have shown that recent models based on discrete descriptions of the cytoskeleton are based on misconceptions. I have proposed an alternative continuous model based on the idea that to achieve action at a distance forces must propagate through the cytoskeleton in a focused way and that this is possible if considerable regions in the cytoskeleton must accommodate isostatic-like solutions. I then went on to analyse the structural characteristics that cytoskeletons should possess in order to accommodate such solutions and control the channeling of forces from the outskirts of the cytoskeleton to regions near the nucleus. A paper entitled "Isostaticity and controlled force transmission in the cytoskeleton - a model awaiting experimental evidence", describing this model, has appeared in The Biophysical Journal. (Dec 05)
• Stress transmission in heterogeneous granular materials - All the above direct solutions to the isostaticity stress equations, as well as those in the literature, have been obtained for ideal media whose fabric tensors are homogeneous. M. Gerritsen, G. Kreiss and I have managed to derive recently solutions for two-dimensional materials whose fabric tensors vary in space. Significantly, the introduction of heterogeneity gives rise to new phenomena that have not been common in the ongoing discussion about isostatic systems. The first is not surprising: force chains can meander in the plane. Since every force source spawns in two dimensions two force chains that bound a 'cone of influence' then these cone boundaries are no longer smooth. Nevertheless, due to the linearity of the equations, 'cones of influence' originating from different sources pass through one another without interaction or scattering. The second phenomenon is that stresses and forces attenuate along force chains. The third is that force chains coming from the same source point become couple due to the heterogeneity and stresses from the chains 'leak' between them into the cone of influence. The amount of leakage depends on the local gradients of the fabric tensor. Finally, when there is a sharp gradient in the fabric tensor, a local branch in the main force chain may appear, giving rise to force chain splitting. Thus, main force chains become parents to secondary force chains, which in principle can parent tertiary force chains and so on. These results have been reported recently in a preprint "Stress chain solutions in two-dimensional isostatic granular systems: fabric-dependent paths, leakage and branching", submitted to Phys. Rev. Lett. and a detailed paper "Analysis of stresses in two-dimensional isostatic granular systems", submitted to Physica A. (Dec 07)
• Rheology of dense granular materials - From statics to dynamics. Flows of macroscopic solid objects are ubiquitous in nature and in technology. In particular, disruption in transport of industrial products causes losses of billions of dollars. Examples of such flows can be found in the pharmaceutical, chemical industry, food and agricultural industries, in energy production and the environment, in the way sand flows in the hourglass and grains in silos. While we have well-established equation for the flow of conventional Newtonian fluids, getting the modelling of granular flow to the same state of the art has proved extremely difficult. Moshe Schwartz, Sam F. Edwards, and I have decided to apply a new approach to the problem and start with a minimal flow model. In this model, a volume element conventionally obeys Newton's laws of motion, but the drag that it experiences from neighbouring elements follows solid friction laws rather than the traditional viscosity term. The problem with this term is that it is non-analytic in that it may increase up to a threshold without the volume elements moving relative to one another and once a threshold is reached relative motion commences.
  It was my idea to call such fluids da Vinci fluids and I take full responsibility for this presumption. My motivation was to honour Leonardo da Vinci for being the first on record to discover and formulate two of the three peculiar laws of solid friction in the mid 1500's. Let me elaborate. In a well documented series of experiments, now existing the British Library in the Codex Arundel, he has found that the friction between two dry solids is (i) independent of the area of contact between them and (ii) is proportional to the force (e.g. weight) that they are pressed against one another. Guillaume Amontons rediscovered these laws in 1699, presumably without knowing about da Vinci's work, which by then had been scattered around the world. Amontons' result were not accepted immediately and it took another eighty years for these laws to be confirmed experimentally by none other than the Charles-Augustin de Coulomb. Coulomb has also discovered the third peculiar feature of solid friction - it does not depend on the relative velocity between the solids in contact. It is in honour of this less well-known original work of da Vinci that I have decided, against non-negligible opposition I should add, to call these da Vinci fluids.
  We have first formulated the equations for discrete system and analysed a range of such systems in rectangular and cylindrical geometries. On solving the equations in simple geometries, we have found that da Vinci fluids generically form plug regions - a well known phenomenon in dense granular flow. We have analysed the formation and development of plug regions gaining much insight into this phenomenon from our minimal model. In particular, we calculated the rate of growth of plug regions, once they have nucleated (where we predict they should), and found that the rate of plug expansion is always proportional to a a one third power of time (t^{1/3}). Furthermore, we have shown that this growth rate is independent even of dimensionality - it is true both in two and in three dimensions.
  Next, we managed to write the continuum equations for the same fluid and verify that they display the same behaviour of plug formation and growth.
  We have several Papers on the subject, one of which has appeared in print, "da Vinci fluids, catch-up dynamics and dense granular flow", one is going to appear in Granular Materials in 2011, and further two on derivation of the flow equations from first-principles and on the fascinating flow in a cylindrical Couette flow. The latter prompted the following Limerick, which summarises the phenomenon of appearance of 'plug regions' in such flows
  
  On Couette flow of da Vinci fluids
  O' whirling sands in the cylinder flow
  Layer by streamline they clump and they slow
  Grains rub their neighbour
  Dissipating much labour
  And da Vinci fluids explain it, gung-ho!
  (RB November 2010)
  
  Here is another Limerick on the basic principles of the da Vinci fluid model
  
  On the da Vinci fluid model
  O' flowing sands in the vessel they jitter
  Layer by layer they rub and they clutter
  Grains densely contact
  Streamlines interact
  And da Vinci fluids make sense so much better
  (RB November 2010)
  
  On da Vinci Shear Flow
  Confine grains between plates and let go
  Layer by layer they shear and they flow
  Grains bump many neighbours
  They rub and they labour
  And da Vinci fluid explain it merveilleux!
  (RB February 2012)
  
  
• Stress transmission in real granular materials follows a new Stato-elasticity theory -
  
  On Stato-elasticity I
  Some put their faith in Elasticity
  Others swear on Isostaticity
  But I stand before you
  To tell you boldly
  That Stato-elasticity is the one and only
  (RB April 2008)
  
  On Stato-elasticity II
  A theory called Elasticity
  Was challenged by Isostaticity
  But I tell you boldly
  That real packs mostly
  Should follow Stato-elasticity
  (RB April 2008)
  
  Since the mid-nineties here has been a raging debate in the community and in the literature on the modelling of stress transmission in granular materials, with two main camps. One camp maintaining that good old elasticity theory should suffice to describe stresses in granular materials and the other claiming that isostaticity theory is the correct description. The main advantage of the latter is that it produces stress field equations that, as discussed above, give rise to characteristics that can be associated with force chains, but its main disadvantage is that real granular materials are normally not isostatic under static conditions (although they may be under dynamic conditions). Elasticity theory, which gives rise to elliptic stress equations, has a major advantage in that it is well studied. However, its big disadvantage is that it cannot explain force chains without resorting to highly anisotropic local elastic constants. In my 2004 paper, I have proposed that real granular materials are in fact two-phase composites: part isostatic and part more conventional solids, perhaps elastic. The basis for this proposal is that isostaticity relies on a very low mean coordination number on the particle level that makes the system statically determinate for the purpose of determining the inter-granular contact forces. In the experiment described above, it has been shown that such isostatic states (there named marginally rigid states) can be approached as close as one wishes in real systems. Very importantly, it has been also shown that an isostatic state is critical in the sense that a particular response length seems to diverge. This is the typical range of the stress response. This length gets shorter as the granular-level connectivity increases above the marginal rigidity value. My argument is that, since real granular materials are formed dynamically, then the final static packing may contain 'quenched' regions of isostatic structures, in which isostaticity theory governs the stress transmission. These quenched states give rise to the force chains observed in real materials, e.g. such as those seen in Behringer experiments, and give rise to the composite nature of real granular materials. The closer the mean granular-level connectivity is to the marginally rigid state, the larger the iosostatic regions. Assuming, for simplicity, that elasticity theory describes stresses in any region that is over-connected (not necessarily true, but useful to simplify analyses), then in these composites both elasticity and isostaticity theories describe stress transmission, each in the corresponding regions. This provides us with a new framework for understanding stress transmission in granular materials. Together with G. Kreiss and M. Gerritsen I have been working to derive stress solutions for such systems - both explicitly for simple geometries and more generally for mildly heterogeneous media. (Jan 08)



• Pullout of single polymer and protein chains, polymer dynamics near the glass temperature and implications to polymer science and protein folding
  
  Polymer Chain Pullout with AFM
  Pick a polymer chain with the tip
  Bond it tight, don't let it slip
  It pulls out in a stutter
  Here a jump, there a flutter
  Thus, through the tube it would not zip
  (RB April 2006)
  
  A great deal of effort has been devoted recently to understanding experiments of pulling single poly mer and biological molecules and measuring the forces involved. These experiments reveal a very rich behaviour and one usually aims to understand from the force fluctuations the structure of the molecule or the dynamics of the pulling process. Understanding these dynamics, however, gives insight into many phenomena in polymer and protein science. I have constructed a theoretical model [1], [2], [3] to understand the dynamics of such processes in the vicinity of the glass transition temperature. I currently explore the implications of my model on viscosity measurements in this regime, with the rather ambitious goal of trying to bridge between the melt- and glass-based models for polymer dynam ics. This model also has direct implications for resistance of polymeric materials to failure at interfaces, plastic deformation of polymer glasses, strength of welded and grafted polymers, and relaxation of single molecules. Efforts to test these ideas experimentally are under way. I am also interested in the application of my model to the pullout of protein chains. There are currently several groups in the world using an Atomic Force Microscope setup to measure the forces needed to unfold particular molecules with the aim to understand from these experiments how proteins are structured. I am keen on applying my model to understand these experiments and hopefully to correctly interpret the force signatures so as to extract information, not only on the protein structure, but also on the relevance of the unfolding dynamics to the folding process of the particular proteins and to protein folding in general.



• Moving curves in 3d and nonlinear dynamics of domain-wall solutions
  
  O' Wiggling Curve
  O' wiggling curve in space she dances
  Domain by kink its tangent prances
  The normal twists
  The binormal tilts
  And in the theory I've made advances
  (RB May 2006)
  
  
  This project is relevant to a surprisingly wide range of issues: Geometric phases; spin chains (eg, the one dangling from your cursor which has one domain wall marked by a ball); protein dynamics; domain formation in thin magnetic layers; and quite a few others. I have some very intriguing results but hardly any time to build up a detailed file here. Hopefully, I will get down to that shortly. In the meanwhile you can look up the following papers: 1. General curve evolution, 2. Multi-twist solutions in magnetic systems, 3. Strange dynamics of domain walls and periodic stripes along classical antiferromagnetic chains. 4. Exact multi-twist solutions for Heisenberg spins on an elastically deformable cylinder, and 5. Dynamics of twists on antiferromagnetic spin chains: Theory.
  Below is an interesting evolution of stripes along a closed antiferromagnetic chain into a periodic structure via a series of domain wall creations. The lines are domain walls and time is the radial coordinate. Any one moment is represented as a particular circle.
  
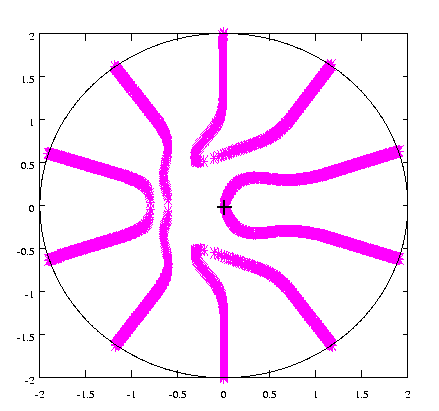
  On magnetic cylinders these solutions correspond to fascinating domain walls. Below are a examples of (from left to right) an instanton, 1, 2, and 3 kinks.
  
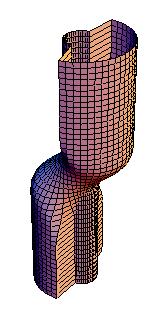
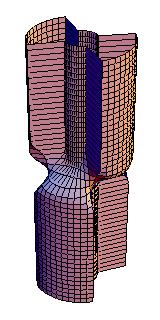
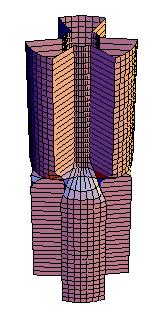
  I have also been toying with the idea to apply my results (and others') on spin chains to ferromagnetic and antiferromagnetic polymers, but this will have to wait until the right collaborator comes along.
  (Collaboration: R. Balakrishnan, A. Saxena)